科學方法的思維模式
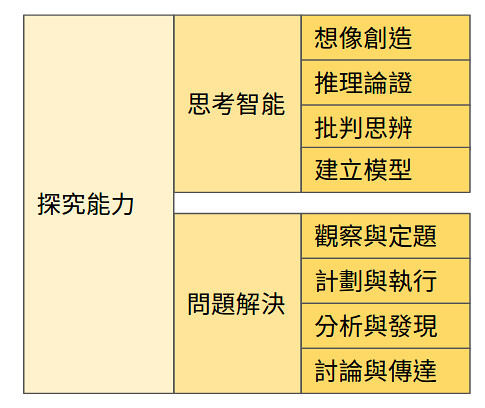
我們熟知的科學方法，其實就是探究能力當中的問題解決那一塊
觀察與定題：觀察、提出問題與假設
計畫與執行：進行實驗
分析與發現：結果分析與結論
至於討論與傳達，在傳統的科學方法論述比較難找到對應，它比較像是把研究結果發表到科學社群，然後社群如何對這議題評斷。
雖然都知道科學方法了，但是我自己也發現，光用科學方法很難去描述這些步驟裡的思維模式，比方說「我知道要提出問題，不過要怎麼提出問題，我應該怎麼去想？」、「我知道要分析結果，不過我要怎麼開始分析，我要用什麼角度去分析？」
這些思維模式很難用科學方法去理解吧，是的，所以探究能力不是只有科學方法這種問題解決的能力而已。課綱裡頭還有思考智能，英文是thinking ability，英文應該比較能理解，就是思考的能力。
它列出了四項：想像創造、推理論證、批判思辨、建立模型。其實思考的能力，當然不只這些，但課綱裡頭只能列出比較重要的來舉出，否則不就一大堆了。
運算思維
而在思考智能這裡，我要另外提一個看起來不在自然課綱裡的東西，但其實就在裡面的，那就是運算思維。
運算思維，英文是Computational Thinking，最近會看到這詞，應該多是資訊科技教育的場合理，比方說程式設計補習班會跟你說要培養孩子的運算思維，科技領域的宣導跟你說我們要培養運算思維，像教育部就有運算思維推動計畫。
運算思維是什麼東西呢？簡單地說，就是一種解決問題的方法和思維模式，是用電腦科學的概念擬定解決方案，而這解決方案是電腦或人腦可理解的，或兩者都可理解的。
其實剛剛我們就已經經歷過了運算思維喔，有想到嗎？在《分析與發現(3)-存儲如何變資料》，我們討論了怎麼整理出乾淨的資料(tidy data)，就是用電腦科學的概念來擬定的。
運算思維的範疇相當廣，因為提出定義和範圍的學者也很多，這是教育部運算思維推動計畫裡的運算思維簡介的簡報之一頁，tidy data我想算是Data collection這個部份。
在這麼多的定義當中，普遍性被認為「啊！那就是運算思維」的有這四個，問題拆解、模式辨別、抽象（摘要）、演算法。我想大部分人跟我一樣，看到這四個字多半會先「啊？」一下。問題拆解我懂，但後面那幾個不太好懂耶，我用成語來解釋一下，應該就比較容易理解了。
問題拆解：化整為零
模式辨別：異中求同
抽象：化繁為簡
演算法：按部就班
問題拆解
問題拆解是化整為零，因為他是將一個大問題拆解成數個小問題，就像是我們今天想去科工館，「要怎麼去？」這是個大問題，我們拆解出好幾個小問題。
- 科工館在哪？
- 有捷運嗎？
- 票價多少？
- 捷運站出來怎麼走？
- 要花多少時間？
- 我要多早出發？
(這些問題，在Google Maps上好像都幫你解決了啊)
模式辨別
模式辨別是異中求同，在龐雜的訊息中，找到相似之處，那個相似之處就是模式(pattern)。就好像犯罪者會有犯罪的模式，警察辦案會尋找的就是那些案件裡是否有一定的模式。
又比如說貓也會有模式，貓的模式是什麼？長長尾巴、有眼睛、有皮毛。雖然這些眼睛、尾巴長得都不一樣，但是你掌握了這個模式，你就知道那是一隻貓。
你會怎麼畫豬呢？一個大圓中間畫一小橢圓，小橢圓裡再畫兩個小圓，雖然我沒直接畫出那是什麼，但是你八成會知道我寫的就是一隻豬的樣子。你為什麼會知道？因為你和我一樣掌握了同樣的豬模式。
有了模式，處理事情就可以很有效率，因為可以用同樣的策略來解決它。比方說收紅包，每個都是飽飽的模式，但是突然拿到一個薄薄的，你就知道這個怪怪的。能夠異中求同，就能夠同中求異，在不疑處有疑。
模式如果不正確，事情就會很麻煩。比方說，你問七年級學生烏龜是不是兩生類，超過一半都會說是，你知道為什麼嗎？因為那就是學生建立的「兩生類模式」，國小時學的叫做兩棲類，國中叫做兩生類，學生建立的兩棲類模式是「可以住水裡，又可以上陸地」，因此只要符合這個模式的，那就叫做兩棲類，所以你可以想想還有什麼動物，會是屬於學生的兩棲類模式？我們又有什麼方法可以讓學生重新建立兩生類模式？
現在的數位相機普遍都有人臉辨識，其實就是能夠它能夠辨識人臉的模式，人腦和電腦辨識人臉用了不太相同的策略，人腦可以把只要有兩顆圓圓的就當作人臉，各位在「face in places
」這個Google圖片搜尋的連結裡看到的圖片，應該都會覺得就是人臉了吧！不過你如果拿相機去拍這些景物，相機可不會把它當作人臉。
抽象
抽象這詞真的很抽象，這叫化繁為簡，也可以叫做摘要，這是聚焦在重要特徵，濾除雜訊與具體細節。
最最最直覺的例子就是地圖，左邊細節超級多的，不過因為我們需要的只有捷運的資訊，所以把那些具體的細節啦、雜訊（地形）通通省略，那就是抽象化的過程。你想想看，難道捷運路線真的長得紅紅一條線，上頭還有一個個圓圈圈嗎？（應該是鐵軌才是吧）
最最最直覺的例子就是地圖，左邊細節超級多的，不過因為我們需要的只有捷運的資訊，所以把那些具體的細節啦、雜訊（地形）通通省略，那就是抽象化的過程。你想想看，難道捷運路線真的長得紅紅一條線，上頭還有一個個圓圈圈嗎？（應該是鐵軌才是吧）
抽象化能幫助我們理解資訊，另一個例子，細胞的樣子，我們會把它抽象化變成黑板畫的簡圖，就一個大圓圈，內部一個小圓圈，那就是抽象了。
演算法
演算法，就是按部就班，是規劃解決問題的詳細步驟。這個很好理解，實驗步驟的流程就是了，我們可以用文字描述，也可以用流程圖去描述。
在程式設計中，我們會將重複使用的部份，另外包裝起來稱為模組。模組化也是運算思維的一部分。
食譜當中的模組有哪些？當我們只要在書上最前面先說「勾芡」就是太白粉加水，後面的食譜，幾乎不用再重講一次，只要說勾芡，你就知道那是什麼了，反正忘記了就回頭翻。「切丁」也是一個，不是說這是切出丁字，這是把食材切成小方塊狀，這同樣是個模組。
我們的實驗步驟裡也有模組啊？有什麼？
「隔水加熱」、「使用顯微鏡觀察」、「製作成玻片標本」
我們在前一階段的實驗中，先訓練學生學會這些技能，將之模組化。接下來我們在實驗步驟中只要提這個詞，就知道那個代表什麼了。
此外，還有平行化，在程式設計時，讓程式同時處理類似或互不干擾的流程。而在實驗流程裡，也會這樣做，像是進行某些加熱實驗時，我們會安排在加熱過程中，順道進行別的工作。或是同步測量兩種溶液的溫度，或是同時測量某個燈泡的電流、電壓值。
而不是測完一個，再測另一個，理解平行化的同步處理優點，就可以有效率地解決問題。
看到這邊，你是不是有發現「啊哈，原來這些就是運算思維啊，其實我也有用到啊」，下一篇來介紹幾個我們在科學實驗上，實際進行的運算思維範例。
