生物課本講到遺傳時,必作的活動就是每個同學拿七個性狀互相比較,看看同學之中有沒有人跟班長一樣。作這實驗時,不一定都要跟班長比,你也可以帶學生跟同學互相比較,看看全班同學,誰和誰一樣?這樣會比跟班長比更好玩喔!
轉換成性狀數字
不過要讓同學同時互相比較這七組性狀,就必須要改一點活動設計才有辦法方便的比。作法是這樣的,把七個性狀轉換成二進位數字,然後再轉成十進位,這樣每個人就會有一個數字,用來表示這七個性狀的組合。
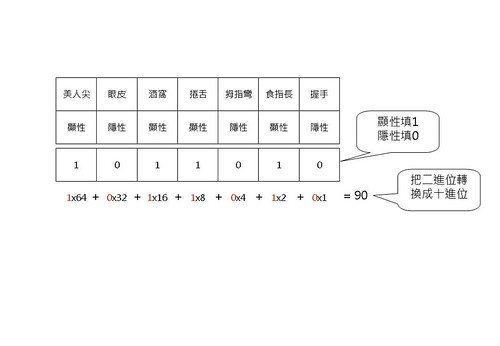
舉個例子來說吧,(看下圖)假設有個人他眼皮、拇指彎和手握起來的樣子是隱性的,其它的都是顯性的。那麼依照性狀的順序,把顯性寫成1,隱性寫成0,他就會有一組數字是1011010,接下來再把這組數字當作二進位來看,把它轉換成十進位,如此他這些性狀的組合,就會是90這個數字。
如此一來,光是用這個性狀數字,就可以很方便地比較每個人是否有相同的性狀組合了,這只要每個人輪流講自己的性狀數字就可以了。
有人會相同性狀嗎?
以班上30個同學來看,如果我跟你打賭這其中至少有兩個人的性狀數字會相同(意思就是有人這七個性狀會相同),你願不願意跟我賭?輸了請贏的一杯飲料。
通常大家會覺得應該值得賭看看,因為7個性狀一共會有2的7次方個組合,一共是128個組合,可是教室裡只有30個,直覺來看,會相同的機率應該很小吧?
不過實際上,30個同學當中,會有兩個人有相同性狀的機率大約是97.5%,很不可思議吧。
以我班上的實際例子來看,30個人當中具有相同性狀的一共有5組同學,有幾組甚至有3人的性狀都一樣,機率很高吧!
如果換一個問題來問,教室裡要有多少人,才能有至少一半的機會,至少有兩個人有相同性狀?
要很多嗎?其實不用,只要14個人就可以了。
意思就是說只要有14個人,就至少有一半的機會,有兩個人會擁有相同性狀;30個人的話,機會就會增加到97.5%;如果以一般教室裡的學生數34或35來看,機率已經接近100%。
也就是說在各位的教室裡,一定會有至少兩個人擁有相同的七個性狀。只是以前你都是用「跟班長像不像」這個方式在比較,所以你可能沒感覺真的會有人一樣。但是如果你換成每個人都互相和同學比較的話,那你就會發現這個有趣的現象。
其實這只要用高中的機率問題來計算就好了。不過很多人離開高中數學太久了,所以可能有點忘記怎麼算,其實我一時也忘記怎麼算,後來是看鄭惟厚教授的【你不能不懂的統計常識】,才因此恍然大悟,為什麼班上隨隨便便都可以找到7個性狀相同的人。
鄭教授在書中舉的例子是生日問題,其實跟我們性狀問題是一樣的,只是生日會有365種可能,七種性狀會有128種可能。我只要依樣畫葫蘆就可以計算出來我要的答案了。
以下說明為什麼教室裡只要有14個學生,就會有一半的機會,會有兩個人相同性狀。

這個表是說明,在多少人數的時候,會有多少機率有相同性狀。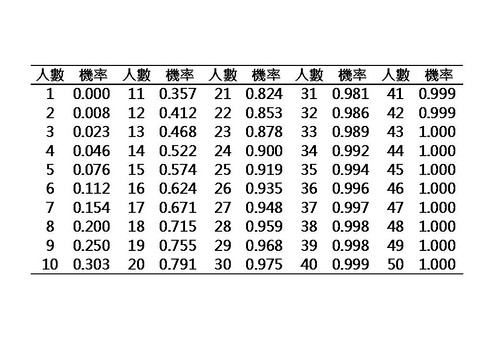
算這種機率問題,我是在excel寫VBA去計算,VBA的程式是這樣的,有興趣的可以自己複製回去玩玩看。
可能有人會想,七個性狀就很容易相像了,那性狀多一點是不是還很容易相像呢?
用程式跑一下就知道了,如果有20個性狀,在35個人當中,就只剩下0.05%的機率會有人相同啊。
而我們性狀如此多,所以真要找到有人跟你相同性狀特徵的。那機率實在很低啊!

轉換成性狀數字
不過要讓同學同時互相比較這七組性狀,就必須要改一點活動設計才有辦法方便的比。作法是這樣的,把七個性狀轉換成二進位數字,然後再轉成十進位,這樣每個人就會有一個數字,用來表示這七個性狀的組合。
舉個例子來說吧,(看下圖)假設有個人他眼皮、拇指彎和手握起來的樣子是隱性的,其它的都是顯性的。那麼依照性狀的順序,把顯性寫成1,隱性寫成0,他就會有一組數字是1011010,接下來再把這組數字當作二進位來看,把它轉換成十進位,如此他這些性狀的組合,就會是90這個數字。

如此一來,光是用這個性狀數字,就可以很方便地比較每個人是否有相同的性狀組合了,這只要每個人輪流講自己的性狀數字就可以了。
有人會相同性狀嗎?
以班上30個同學來看,如果我跟你打賭這其中至少有兩個人的性狀數字會相同(意思就是有人這七個性狀會相同),你願不願意跟我賭?輸了請贏的一杯飲料。
通常大家會覺得應該值得賭看看,因為7個性狀一共會有2的7次方個組合,一共是128個組合,可是教室裡只有30個,直覺來看,會相同的機率應該很小吧?
不過實際上,30個同學當中,會有兩個人有相同性狀的機率大約是97.5%,很不可思議吧。
以我班上的實際例子來看,30個人當中具有相同性狀的一共有5組同學,有幾組甚至有3人的性狀都一樣,機率很高吧!
如果換一個問題來問,教室裡要有多少人,才能有至少一半的機會,至少有兩個人有相同性狀?
要很多嗎?其實不用,只要14個人就可以了。
意思就是說只要有14個人,就至少有一半的機會,有兩個人會擁有相同性狀;30個人的話,機會就會增加到97.5%;如果以一般教室裡的學生數34或35來看,機率已經接近100%。
也就是說在各位的教室裡,一定會有至少兩個人擁有相同的七個性狀。只是以前你都是用「跟班長像不像」這個方式在比較,所以你可能沒感覺真的會有人一樣。但是如果你換成每個人都互相和同學比較的話,那你就會發現這個有趣的現象。
其實這只要用高中的機率問題來計算就好了。不過很多人離開高中數學太久了,所以可能有點忘記怎麼算,其實我一時也忘記怎麼算,後來是看鄭惟厚教授的【你不能不懂的統計常識】,才因此恍然大悟,為什麼班上隨隨便便都可以找到7個性狀相同的人。
鄭教授在書中舉的例子是生日問題,其實跟我們性狀問題是一樣的,只是生日會有365種可能,七種性狀會有128種可能。我只要依樣畫葫蘆就可以計算出來我要的答案了。
以下說明為什麼教室裡只要有14個學生,就會有一半的機會,會有兩個人相同性狀。

這個表是說明,在多少人數的時候,會有多少機率有相同性狀。

算這種機率問題,我是在excel寫VBA去計算,VBA的程式是這樣的,有興趣的可以自己複製回去玩玩看。
Sub Macro1()
trait = 2^7
For n = 1 To 50
q = 1
For i = 0 To n - 1
q = q * (trait - i)
Next
p = 1 - q / (trait ^ n)
Cells(n, 1) = n
Cells(n, 2) = p
Next
End Sub
可能有人會想,七個性狀就很容易相像了,那性狀多一點是不是還很容易相像呢?
用程式跑一下就知道了,如果有20個性狀,在35個人當中,就只剩下0.05%的機率會有人相同啊。
而我們性狀如此多,所以真要找到有人跟你相同性狀特徵的。那機率實在很低啊!
