2013年時,我玩了一個叫做鏡筒玩玩變形畫anamorph的東西
以影像的放大來舉例
原始影像在x方向放大a倍,在y方向放大b倍,新影像可以表示為:
x' = ax
y' = by
就可以用原始影像算出新影像應該長什麼樣子,
舉例來說,原始影像在x方向和y方向都放大2倍,
那麼原始影像的(1,1)和(1,2)就會變成新影像的(2,2)和(2,4)兩個點的顏色,
但是新影像的(2,3)呢?原始影像並沒有(1,1.5)這個點啊,所以那個點就會沒有顏色。所以實作上就會用inverse mapping 來處理。
原本的方程式可以改寫成
x = x' /a
y = y' /b
再透過一些內插法(Interpolation)就可以計算新影像應該是什麼顏色。例如剛剛的問題,新影像的(2,3)的顏色就是原始影像的(1,1.5)的顏色。如果使用Near Neighbor Interpolation,就用原始影像的(1,2)來代表(1,1.5),如果是用Bilinear Interpolation,就用原始影像的(1,1)和(1,2)的顏色算平均得到(1, 1.5)的顏色,然後在指定給新影像的(2,3)。
接下來再來思考這種鏡筒變形畫怎麼製作吧。
鏡筒變形畫
原始影像長這樣
也就是要先將原始影像的座標從笛卡爾座標變成極座標,然後在極座標上進行幾何轉換。
原始影像的紅點和藍點都在同一個x座標上,經過變換後,它們的極座標都會在同樣的θ 上,而它們的r由它們的y座標決定,y座標越小,則r越大,像是變換後的紅點會移動到最外圍。以藍點為例,原始的y座標是影像高度的4/7,變換後的r就是 r0 + r1(4/7)
原始影像的紅點和綠點在同一個y座標上,變換後它們的 r 都一樣,而θ則不相同,由原始影像的x座標決定。
用數學方程式表達這種變換如下:
根據這樣的原理所撰寫的程式在github
https://github.com/ChihHsiangChien/anamorph
其中的anamorph.py 就是產生變形畫的程式
定義參數:
f(x, y):原始影像的像素值。r0:定義影像的初始半徑。r1:定義影像的變換範圍半徑。θ:角度座標,用來決定像素的旋轉。r:半徑座標,用來決定像素的距離。(x0, y0):中心點的坐標。nx, ny:原始影像的寬度和高度。
變換步驟:
1. 極座標轉換:
r = √((x - x₀)² + (y - y₀)²)
θ = arctan2(y - y₀, x - x₀)
其中 (x₀, y₀) 是新影像的中心,x 和 y 是新影像的坐標點。
2. 新座標映射:
新的橫坐標 map_x 和縱坐標 map_y 是透過角度 θ 和半徑 r 映射回原始影像的座標:
map_x = nx - 1 - (nx - 1) · (θ + π) / 2π
map_y = ny - 1 - (ny - 1) · (r - r₀) / r₁
這些公式將極座標 r 和 θ 重新映射到原始影像的笛卡爾坐標 (map_x, map_y),然後將原影像進行扭曲或展開。
3. 有效區域檢測:
使用mask來確保映射後的像素點在有效範圍內:
valid_mask = (map_x ≥ 0) ∧ (map_x < nx) ∧ (map_y ≥ 0) ∧ (map_y < ny)
4. 生成新影像:
將原影像的有效像素根據映射後的座標填充到新影像中,無效區域使用白色填充。
根據這樣的原理所撰寫的程式在github
https://github.com/ChihHsiangChien/anamorph
其中的anamorph.py 就是產生變形畫的程式
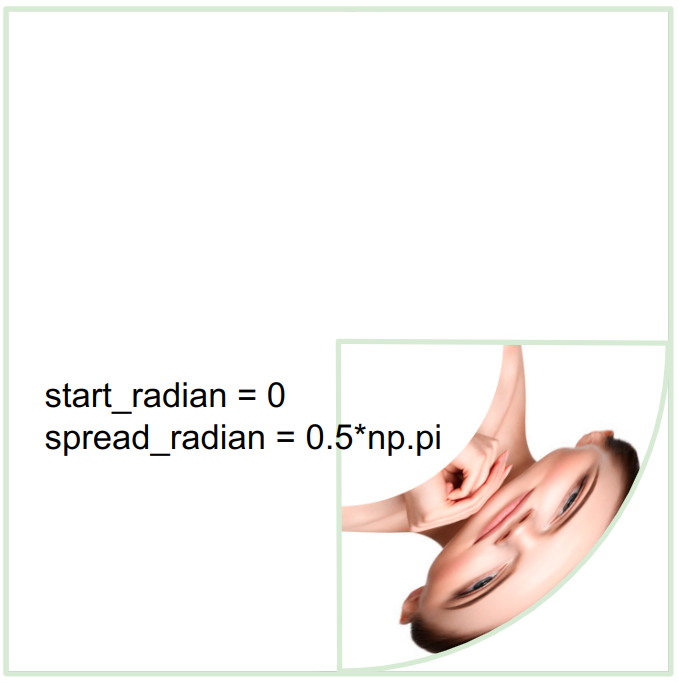
其中有兩個參數start_radian 和 spread_radian ,指定的數值是弧度,為np.pi的倍數
start_radian = np.pi時,弧形的起點從np.pi的方向開始畫,開展的弧度是0.5π = 90°