這些在討論松果、鳳梨、花瓣或是向日葵小花怎麼排的問題,其實和葉子怎麼在莖上長,都是相同的問題。
學植物分類的時候,會學到葉子在莖上的生長方式,包括了對生、十字對生、互生和輪生等等。這些葉子的排列方式有個有趣的規則,特別是互生。
有機會看到互生的葉子,不妨看看葉子是怎麼長的,互生並不是單純的左長一片、右長一片,其實每片葉子之間會夾了一個特別的角度,像下面的這個例子,每片葉子的角度大約是夾了120度。
若是把最底下的葉子當作0號,那麼往上陸續編成1號、2號、3號,編到第3號的時候,第3號的葉子剛好和第0號是同一個位置角度,也就是3片葉子沿著莖繞了1圈。我們可以把這樣的葉序稱為1/3(繞1圈要3片葉子)。
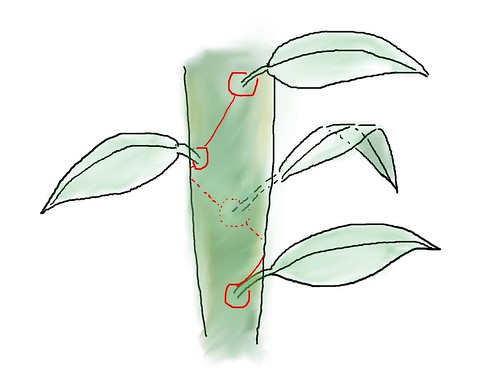
有些是要5片才能繞2圈,這樣的葉序比稱為2/5,有些是8片繞3圈,這個葉序比是3/8
把這些數字整理一下之後,就會發現和費氏數列還有點關係呢。
費氏數列是1 1 2 3 5 8 13 ...,剛剛出現的葉序是1/3 2/5 3/8,剛好都在這裡頭。
1/3的葉序比,每片葉子夾120度
2/5的葉序比,每片葉子夾144度
3/8的葉序比,每片葉子夾135度
每片葉子夾了100多度是有好處的。從上俯瞰,就會發現夾這樣的角度,可以讓葉子不會互相重疊在一起。
其實這樣的葉序比和馬鈴薯芽眼有關係耶,有人知道,馬鈴薯的芽眼可以相連變成螺旋狀嗎?
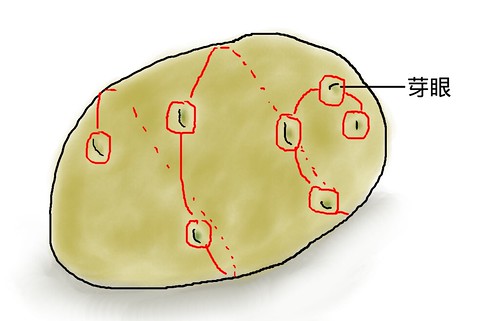
其實只要知道馬鈴薯是莖,就可以理解這個螺旋狀是怎麼出現的了。
前面才講過葉序比嘛,我們找個植物的莖,標示它們上面的葉子生長位置,也可以畫出個螺旋狀。而馬鈴薯也是莖嘛!不過是個縮短肥胖的莖,而上面的芽眼自然也就可以畫出像一般莖一樣的螺旋狀。
那接下來想想,在一般莖上畫的螺旋,最後會螺旋到哪裡?那個中心最後到的是莖的頂端。那麼,馬鈴薯呢?螺旋的中心也就是莖頂啦。

馬鈴薯最早發芽的地方,就是在莖頂的那個螺旋中心,那裡也就是頂芽的位置。
因為頂芽優勢,所以其他側芽長得都會比較慢,不過我曾經看過一本講science project的書,介紹了一個可以抑制馬鈴薯頂芽優勢的方法,讓馬鈴薯每個芽都發芽,方法也很簡單,等我試了之後再來介紹吧。