這兩天的天文大事件是冬至前的月食發生。
我到很大的時候才意會到,雖然月食和月亮每月的變化一樣,都有圓缺。但是兩者缺的形狀其實是不同的。前者會缺是因為地球的影子,後者會缺是因為地球上看月球被照亮的位置不同。
因為月食是地球的影子造成,所以我就發噗問,是不是可以用月食的情況得知地球是圓的?
經過噗友geo的告知,原來還有人將月食的形狀與移動位置,拼接起來,然後就變成這個樣子了。中間那個大黑影就是地球的影子
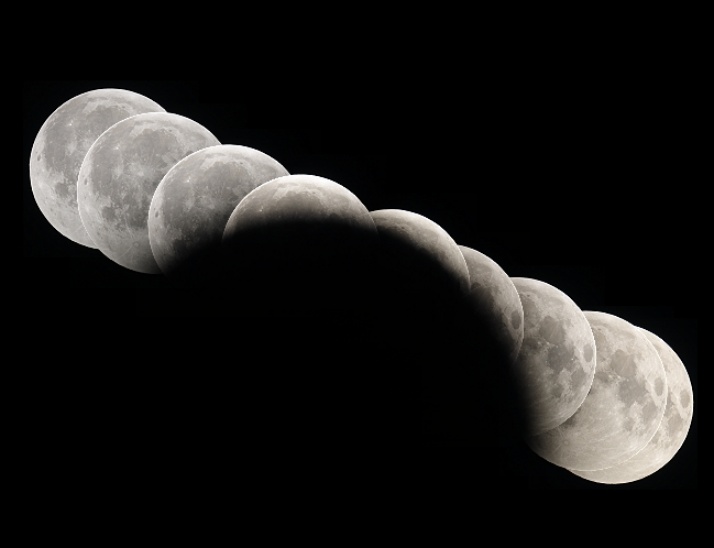
圖片來源:http://apod.nasa.gov/apod/ap080820.html
除了上面那張以外,這張也很經典呢!

心中一直思考著,是不是可以用這影子的曲率、大小等資料來求出地球月亮的距離啊,或是什麼天文上的資料,不過想來想去暫時無解。
但是有件事卻又引起我的注意了,12/22是冬至,那麼冬至是不是除了煮湯圓以外,是不是還有什麼活動可以玩呢?
我們班理化老師還特地在這天舉辦煮湯圓活動,還可以順便教熱對流(到底是順便煮湯圓,還是順便教熱對流啊)
冬至時,太陽直射南迴歸線,正是可以來玩立竿見影測經緯度的好日子啊。
許多人聽到在這天可以做這件事,都非常驚奇。其實道理很簡單,看下圖就知道了。只要知道太陽仰角就可以用簡單的數學計算出待測緯度了,而太陽仰角就是用桿長和影長去計算就可以了。

為了讓我的學生們玩玩這個活動,我發下了一份資料、捲尺和粉筆一隻,要他們冬至時的中午到操場測量,並用數學計算出所在的經緯度。
我的資料是這麼寫的:
學生們必須在操場上找尋適合的杆影來做測量,有些學生選擇用籃球架,有些則是用排球網架。有沒有選到垂直的杆,會影響到最後計算緯度時的正確性。
要計算經緯度必須測量最短的影長才可以,因為此時是太陽過中天的時刻。得到了杆長和最短影長之後,還必須用三角函數tan()去求太陽仰角,不過學生還沒學過三角函數,所以我就直接給他們對照表。
如果要在excel或是calc中計算各仰角對應的杆長/影長比,那麼可以用這個公式
在A1輸入角度,B1輸入 =TAN(A1*PI()/180)
我們學校的經度約是120.9E,所以太陽過中天時,讓杆影最短的時刻,應該是在11:56左右。根據氣象局的資料,新竹地區太陽過中天的時間是 11:54:21
,不過我想這個數據應該是新竹氣象站(在竹北)的時間。
要知道杆影何時最短,得從11點多就開始畫出杆影的位置,這樣才能比較的出來。


學生拿到粉筆就會開始作怪,學生在剛開始測量的時候,突然大叫「老師,有人死了」,過去一看,嗯..就是右上角那個圖形。(刑案現場都有的那個地面人型啊)

冬至的太陽真的很低,即使是中午了,大家的影子也拉得好長一條。這天太陽的仰角大概只有41度左右,非常的低啊。



學生經過測量之後,估算出本校的經緯度數據,六組當中得到以下五個數據
24.5°N 121°E(誤差35.36公里)
24.8°N 121°E(這是最準的,誤差3.32公里)
24.9°N 121°E(誤差9.37公里)
25.3°N 121°E(這個座標已經落海了,誤差53.31公里)
25.8°N 121°E(這個座標也落海了,誤差108.23公里)
我利用Google地圖查詢,學校的經緯度是 24.81°N 120.97°E,看起來大家測得都還蠻準的,至於那些算到25°N以外的,都是用排球網架來做測量,問題出在那個杆子不是垂直地面的啊,所以計算上就會出現比較大的誤差。
這個活動不是只有冬至才能玩,其實二分二至都能玩(春分秋分夏至冬至)
未來還可以在其他的日子來玩玩,所以我就順便一起把其他的圖片畫了備用。
說到春分秋分,其實我辦公室的座位就是春分秋分之位耶,每年只有那兩天的傍晚,陽光才會曬到我的桌上。


隆欽還建議可以將冬至日出或日落時的方位,與春分、夏至、秋分時的方位作比較,或是繪製九九消寒圖,可以和國文課結合。若能再把時間拉長,可用針孔相機拍攝日軌圖。
這個網站(www.solargraphy.com),有介紹如何用針孔相機拍攝日軌圖,原來只要一個黑色底片筒和一張底片就可以拍攝了。不過我有個問題,一張底片要怎麼送去沖?
後記:關於利用影子求方位或是經緯度這件事,其實在儒勒·凡爾納的經典科幻小說神祕島就有過這樣的橋段呢
後記二:立竿見影測經緯這件事,在花蓮女中歐漢文老師的這篇文章-追尋太陽的角度有很詳細的說明。
後記三:有了緯度,其實還可以更進一步計算出地球的周長。
首先利用Google Earth計算本校到赤道的距離,約為2742.86公里
接著利用一個簡單公式
地球圓周x (緯度/360度)=緯度相對應的弧長
所以地球圓周 =2742.86/(24.8/360)=39815.7公里,與實際值非常接近呢!

我到很大的時候才意會到,雖然月食和月亮每月的變化一樣,都有圓缺。但是兩者缺的形狀其實是不同的。前者會缺是因為地球的影子,後者會缺是因為地球上看月球被照亮的位置不同。
因為月食是地球的影子造成,所以我就發噗問,是不是可以用月食的情況得知地球是圓的?
經過噗友geo的告知,原來還有人將月食的形狀與移動位置,拼接起來,然後就變成這個樣子了。中間那個大黑影就是地球的影子

圖片來源:http://apod.nasa.gov/apod/ap080820.html
除了上面那張以外,這張也很經典呢!

心中一直思考著,是不是可以用這影子的曲率、大小等資料來求出地球月亮的距離啊,或是什麼天文上的資料,不過想來想去暫時無解。
但是有件事卻又引起我的注意了,12/22是冬至,那麼冬至是不是除了煮湯圓以外,是不是還有什麼活動可以玩呢?
我們班理化老師還特地在這天舉辦煮湯圓活動,還可以順便教熱對流(到底是順便煮湯圓,還是順便教熱對流啊)
冬至時,太陽直射南迴歸線,正是可以來玩立竿見影測經緯度的好日子啊。
許多人聽到在這天可以做這件事,都非常驚奇。其實道理很簡單,看下圖就知道了。只要知道太陽仰角就可以用簡單的數學計算出待測緯度了,而太陽仰角就是用桿長和影長去計算就可以了。

為了讓我的學生們玩玩這個活動,我發下了一份資料、捲尺和粉筆一隻,要他們冬至時的中午到操場測量,並用數學計算出所在的經緯度。
我的資料是這麼寫的:
身為冒險家的你搭乘『幼幼號』飛機墜落光華百慕達,在2010年12月22日冬至時,你該怎麼知道光華百慕達的經緯度呢?
1.太陽過中天子午線(天上正北正南的連線)的時候,杆影最短,且杆影指向正北方
2.經度可以由太陽過中天的時刻求出。在東經120度的地方,正午12點時,太陽會過中天,而地球自轉一圈為24小時,每圈為360度,意即每分鐘轉0.25度,因此在東經120度更往東的地方,太陽過中天的時間會更早。請由竿影最短的時間,求出光華百慕達的經度。
3.由太陽過中天時的杆長與影長,如何求得當地緯度?下面這張圖可以給你提示。
請根據以上資料估算光華百慕達的經緯度,並寫下計算過程
學生們必須在操場上找尋適合的杆影來做測量,有些學生選擇用籃球架,有些則是用排球網架。有沒有選到垂直的杆,會影響到最後計算緯度時的正確性。
要計算經緯度必須測量最短的影長才可以,因為此時是太陽過中天的時刻。得到了杆長和最短影長之後,還必須用三角函數tan()去求太陽仰角,不過學生還沒學過三角函數,所以我就直接給他們對照表。
如果要在excel或是calc中計算各仰角對應的杆長/影長比,那麼可以用這個公式
在A1輸入角度,B1輸入 =TAN(A1*PI()/180)
我們學校的經度約是120.9E,所以太陽過中天時,讓杆影最短的時刻,應該是在11:56左右。根據氣象局的資料,新竹地區太陽過中天的時間是 11:54:21
,不過我想這個數據應該是新竹氣象站(在竹北)的時間。
要知道杆影何時最短,得從11點多就開始畫出杆影的位置,這樣才能比較的出來。


學生拿到粉筆就會開始作怪,學生在剛開始測量的時候,突然大叫「老師,有人死了」,過去一看,嗯..就是右上角那個圖形。(刑案現場都有的那個地面人型啊)

冬至的太陽真的很低,即使是中午了,大家的影子也拉得好長一條。這天太陽的仰角大概只有41度左右,非常的低啊。



學生經過測量之後,估算出本校的經緯度數據,六組當中得到以下五個數據
24.5°N 121°E(誤差35.36公里)
24.8°N 121°E(這是最準的,誤差3.32公里)
24.9°N 121°E(誤差9.37公里)
25.3°N 121°E(這個座標已經落海了,誤差53.31公里)
25.8°N 121°E(這個座標也落海了,誤差108.23公里)
我利用Google地圖查詢,學校的經緯度是 24.81°N 120.97°E,看起來大家測得都還蠻準的,至於那些算到25°N以外的,都是用排球網架來做測量,問題出在那個杆子不是垂直地面的啊,所以計算上就會出現比較大的誤差。
這個活動不是只有冬至才能玩,其實二分二至都能玩(春分秋分夏至冬至)
未來還可以在其他的日子來玩玩,所以我就順便一起把其他的圖片畫了備用。
說到春分秋分,其實我辦公室的座位就是春分秋分之位耶,每年只有那兩天的傍晚,陽光才會曬到我的桌上。


隆欽還建議可以將冬至日出或日落時的方位,與春分、夏至、秋分時的方位作比較,或是繪製九九消寒圖,可以和國文課結合。若能再把時間拉長,可用針孔相機拍攝日軌圖。
這個網站(www.solargraphy.com),有介紹如何用針孔相機拍攝日軌圖,原來只要一個黑色底片筒和一張底片就可以拍攝了。不過我有個問題,一張底片要怎麼送去沖?
後記:關於利用影子求方位或是經緯度這件事,其實在儒勒·凡爾納的經典科幻小說神祕島就有過這樣的橋段呢
後記二:立竿見影測經緯這件事,在花蓮女中歐漢文老師的這篇文章-追尋太陽的角度有很詳細的說明。
後記三:有了緯度,其實還可以更進一步計算出地球的周長。
首先利用Google Earth計算本校到赤道的距離,約為2742.86公里
接著利用一個簡單公式
地球圓周x (緯度/360度)=緯度相對應的弧長
所以地球圓周 =2742.86/(24.8/360)=39815.7公里,與實際值非常接近呢!
